کنترل کننده PID

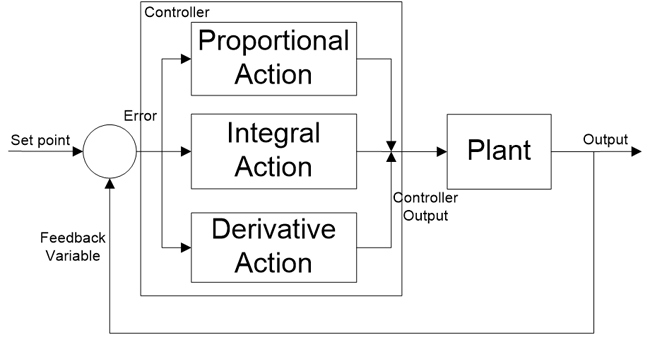
دو نوع سیستم وجود دارد: سیستم حلقه باز و سیستم حلقه بسته، سیستم حلقه باز به‌عنوان سیستم کنترل نشده نیز شناخته می‌شود و سیستم حلقه بسته به‌عنوان سیستم کنترل‌شده شناخته می‌شود. در سیستم حلقه باز، خروجی کنترل نشده است چون‌که در این سیستم فیدبکی وجود ندارد و در یک سیستم حلقه بسته خروجی با کمک کنترل کننده، کنترل می‌شود و این سیستم به یک یا تعداد بیشتری مسیر فیدبک نیاز دارد. یک سیستم حلقه باز بسیار ساده است اما در کاربردهای کنترل صنعتی مفید نیست چون این سیستم کنترل نشده است. سیستم حلقه بسته پیچیده است اما برای کاربردهای صنعتی پراستفاده است چون خروجی این سیستم می‌تواند در یک مقدار موردنظر پایدار باشد. PID مثالی از یک سیستم حلقه بسته است. نمودار بلوکی این سیستم در شکل 2 نمایش داده‌شده است:

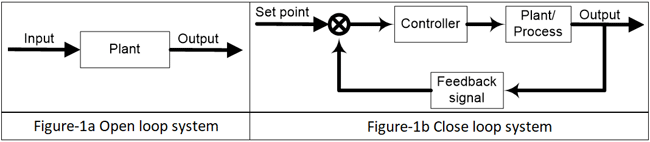
شکل 2: سیستم‌های حلقه باز و حلقه بسته برای کنترل کننده‌ها

یک سیستم حلقه بسته به‌عنوان سیستم کنترل فیدبک نیز شناخته می‌شود و این نوع از سیستم برای طراحی سیستم به‌طور خودکار پایدار، در خروجی موردنظر و یا مرجع، استفاده می‌شود. به این دلیل، آن سیستم یک سیگنال خطا تولید می‌کند.

سیگنال خطا (e(t اختلاف بین خروجی (y(t و سیگنال مبنا (u(t است، وقتی‌که این خطا صفر است به این معنا است که خروجی موردنظر به‌دست‌آمده است و در این شرایط خروجی همانند سیگنال مبنا است.

برای مثال، یک ماشین خشک‌کنی چندین مرتبه که از پیش تعیین‌شده است، کار می‌کند. وقتی‌که ماشین خشک‌کنی روشن می‌شود، تایمر شروع می‌کند و تا زمانی که شمارش تایمر تمام شود، ماشین خشک‌کنی ادامه می‌دهد و خروجی یعنی لباس خشک را می‌دهد. این یک سیستم حلقه باز ساده است که خروجی نیازی به کنترل شدن ندارد و هیچ مسیر فیدبکی لازم نیست. اگر در این سیستم ما از یک سنسور رطوبت‌سنج که مسیر فیدبک را فراهم می‌کند، استفاده کنیم و آن را با نقطه تنظیم‌شده مقایسه کنیم و خطایی را تولید کنیم، ماشین خشک‌کنی تا زمانی به کارش ادامه می‌دهد که این خطا صفر شود. این بدان معناست که وقتی رطوبت پارچه برابر رطوبت تنظیم‌شده است، ماشین خشک‌کنی، کارکردن را متوقف می‌کند. در سیستم حلقه باز، ماشین خشک‌کنی برای زمان ثابتی، صرف‌نظر از این‌که لباس خشک یا خیس است، کار می‌کند. اما در سیستم حلقه بسته، ماشین خشک‌کنی برای زمان ثابتی کار نمی‌کند، ماشین خشک‌کنی تا زمانی که لباس خشک شود، کارمی کند. این فایده سیستم حلقه بسته و استفاده از کنترل کننده است.

کنترل کننده PID و طرز کار آن:

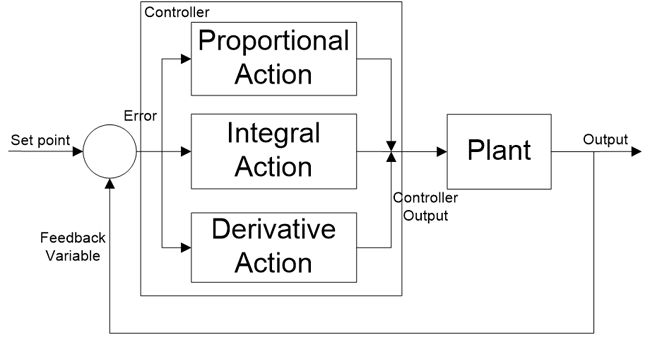
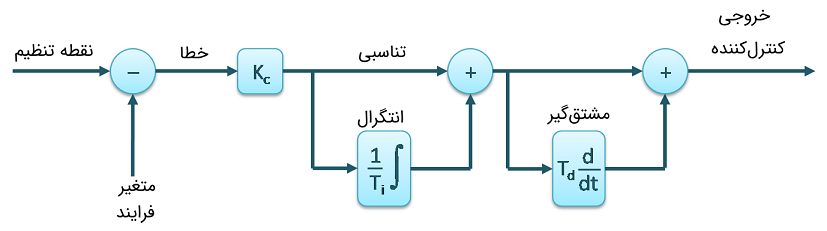
پس کنترل کننده PID چیست؟  کنترل کننده PID در سراسر جهان پذیرفته‌شده است و پرکاربردترین کنترل کننده در کاربردهای صنعتی است، چون‌که کنترل کننده PID ساده است، پایداری خوب و پاسخ سریعی را فراهم می‌کند. PID مخفف عبارت‌های Proportional (تناسب)، Integral (انتگرال)، Derivative (مشتق) است. در هر کاربردی ضریب این سه عملیات برای به دست آوردن کنترل و پاسخ بهینه متفاوت است. ورودی کنترل کننده سیگنال خطا است و خروجی به دستگاه یا فرایند داده می‌شود. سیگنال خروجی کنترل کننده به روشی تولیدشده است که خروجی دستگاه برای رسیدن به مقدار موردنظر تلاش می‌کند.

کنترل کننده PID یک سیستم حلقه بسته است که سیستم کنترل فیدبک دارد و متغیر فرایند (متغیر فیدبک) را با نقطه تنظیم‌شده مقایسه می‌کند و سیگنال خطایی تولید می‌کند و بر طبق آن، خروجی سیستم را تنظیم می‌کند. این فرایند تا اینکه خطا صفر شود یا مقدار متغیرهای فرایند با مقدار تنظیم‌شده برابر شوند، ادامه می‌یابد.

کنترل کننده‌ی PID نتایج بهتری نسبت به کنترل کننده خاموش/روشن می‌دهد. در کنترل کننده خاموش/روشن، تنها دو وضعیت برای کنترل سیستم در دسترس است. آن تنها می‌تواند خاموش و یا روشن باشد. کنترل کننده خاموش/روشن وقتی‌که مقدار فرایند کمتر از نقطه تنظیم‌شده است روشن خواهد شد و وقتی‌که مقدار فرایند بزرگ‌تر از نقطه تنظیم‌شده است، می‌تواند خاموش شود. در این کنترل کننده خروجی هیچ‌وقت پایدار نمی‌شود، خروجی همیشه در حدود نقطه تنظیم‌شده نوسان می‌کند. اما کنترل کننده PID نسبت به کنترل کننده خاموش/روشن دقیق‌تر و پایدارتر است.

کنترل کننده نوع P:

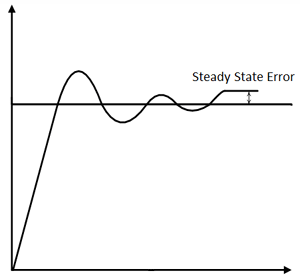
P با مقدار واقعی خطا متناسب است. اگر خطا بزرگ باشد، خروجی کنترل کننده هم بزرگ است و اگر خطا کوچک باشد خروجی کنترل هم کوچک است اما ضریب بهره Kp است. همچنین در نظر بگیرید، سرعت پاسخ هم به‌طور مستقیم با ضریب بهره تناسبی (Kp)، متناسب است. بنابراین سرعت پاسخ با افزایش مقدار Kp زیاد می‌شود اما اگر Kp بیش از محدوده معمول افزایش یابد، متغیر فرایند شروع به نوسان کردن در سرعت بالا می‌کند و سیستم را ناپایدار می‌سازد.

اگر کنترلر فقط تناسبی باشد سیگنال ERRORدر ضریب تناسبی که KP یا GAIN گفته میشود ضرب شده و سیگنال فرمان تولید میشود.بنابراین خروجی متناسب با ورودی طبق رابطه زیر تغییر میکند.

m =kpe +b

(y(t) ∝ e(t

(y(t) = k_p * e(t

کنترل کننده نوع I انتگرال گیر:

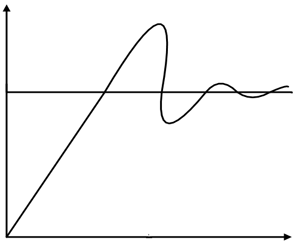
به‌طورکلی کنترل کننده انتگرالی برای کاهش خطای حالت پایدار استفاده می‌شود. I، انتگرال (نسبت به زمان) مقدار واقعی خطا است، به سبب انتگرال‌گیری، مقدار خطای بسیار کمی، پاسخ انتگرالی بسیار بزرگی را نتیجه می‌دهد. عملیات کنترل کننده انتگرالی ادامه می‌یابد تا خطا صفر شود.

(y(t) ∝ ∫ e(t)y(t) = k_i ∫ e(t

که Ki، یک عامل بهره تناسب است.

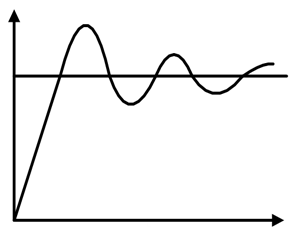
بهره انتگرال با سرعت پاسخ‌گویی رابطه معکوس دارد، افزایش Ki، سرعت پاسخگویی را کاهش می‌دهد. کنترل کننده‌های انتگرالی و تناسبی به‌طور ترکیبی (کنترل کننده PI) برای پاسخ پایدار و سرعت پاسخ خوب، استفاده می‌شوند.

کنترلر کننده مشتق گیر D:

کنترل کننده مشتق گیر به‌صورت ترکیب PD و یا PID استفاده می‌شود. کنترل کننده مشتق گیر هیچ‌گاه به‌تنهایی استفاده نمی‌شود چون اگر خطا ثابت (غیر صفر) باشد، خروجی کنترل کننده صفر خواهد شد. در این وضعیت، کنترل کننده مانند حالت خطای صفر رفتار می‌کند، اما درواقع مقداری خطا (ثابت) وجود دارد. همان‌طور که در رابطه نشان داده‌شده است، خروجی کنترل کننده مشتق گیر رابطه مستقیمی با سرعت تغییر خطا نسبت به زمان دارد. با حذف علامت تناسب، ما به ثابت بهره مشتق (Kd) می‌رسیم. به‌طورکلی کنترل کننده‌های مشتق گیر زمانی استفاده می‌شوند که متغیرهای فرایند شروع به نوسان کنند یا تغییرات در سرعت بسیار بالا داشته باشند. کنترل کننده‌های مشتقی همچنین برای پیش‌بینی عملکرد آینده خطا، به‌وسیله‌ی منحنی خطا استفاده می‌شوند. رابطه ریاضی به‌صورت نشان داده‌شده در زیر است:

y(t) ∝ de(t)/dty(t) = K_d * de(t)/dt

که Kd یک عامل بهره تناسب است.

کنترل کننده نوع PI :

این کنترل کننده، ترکیب کنترل کننده I و P است. همان‌طور که در معادله ریاضی زیر نشان داده‌شده است، خروجی کنترل کننده جمع پاسخ‌های انتگرالی و تناسبی است.

y(t) ∝ (e(t) + ∫ e(t) dt)y(t) = kp *e(t) + ki ∫ e(t) dt
خطای ماندگار آن به خاطر وجود عنصر I ناچیز است.

کنترل کننده مشتقی و تناسبی (PD):

این کنترل کننده ترکیب کنترل کننده‌های P و D است. خروجی کنترل کننده مجموع پاسخ‌های مشتقی و تناسبی است. رابطه ریاضی کنترل کننده PD در زیر نمایش داده‌شده است.

y(t) ∝ (e(t) + de(t)/dt)y(t) = kp *e(t) + kd * de(t)/dt
سرعتش به خاطر عنصر D بالاست .در لوپ هایی که ماهیت انها کند است مثل لوپ دما کاربرد دارد.

کنترل کننده تناسبی، انتگرالی و مشتقی ( PID ):

این کنترل کننده ترکیب کنترل کننده‌های P، I و D است. خروجی کنترل کننده مجموع پاسخ‌های تناسبی، انتگرالی و مشتقی است. رابطه ریاضی کنترل کننده PID در زیر نمایش داده‌شده است.

y(t) ∝ (e(t) + ∫ e(t) dt + de(t)/dt)y(t) = kp *e(t) + ki ∫ e(t) dt + kd * de(t)/dt